[BOJ/C++] 1003 피보나치 함수 / 효율적인 메모이제이션
다음 소스는 N번째 피보나치 수를 구하는 C++ 함수이다.
int fibonacci(int n) {
if (n == 0) {
printf("0");
return 0;
} else if (n == 1) {
printf("1");
return 1;
} else {
return fibonacci(n-1) + fibonacci(n-2);
}
}fibonacci(3)을 호출하면 다음과 같은 일이 일어난다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
- fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
- 두 번째 호출한 fibonacci(1)은 1을 출력하고 1을 리턴한다.
- fibonacci(0)은 0을 출력하고, 0을 리턴한다.
- fibonacci(2)는 fibonacci(1)과 fibonacci(0)의 결과를 얻고, 1을 리턴한다.
- 첫 번째 호출한 fibonacci(1)은 1을 출력하고, 1을 리턴한다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1)의 결과를 얻고, 2를 리턴한다.
1은 2번 출력되고, 0은 1번 출력된다. N이 주어졌을 때, fibonacci(N)을 호출했을 때, 0과 1이 각각 몇 번 출력되는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다.
각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. N은 40보다 작거나 같은 자연수 또는 0이다.
출력
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
[풀이]
피보나치 수열에서 0과 1이 호출되는 횟수를 구하는 문제다. 답은 문제에 제시된 코드를 이용해 간단하게 구할 수 있으나, 제한시간이 관건이다. N이 40미만으로 제한되어 있다고 해도, fibonacci(39)를 돌려보면 재귀함수의 특성으로 인해 수행시간이 굉장히 느려진다는 것을 알 수 있다. 피보나치 수열을 빠르게 구하는 여러 방법 중에 메모이제이션 방법을 사용했는데, 반복해서 같은 함수를 부르지 않도록 코드를 수정해 최대한으로 수행시간을 줄였다.
[코드]

결과를 보면 알겠지만 시간이 어디까지 허용되는지 알아내기 위해 많은 코드 수정을 거쳤다. 답이 궁금한 사람은 가장 마지막 코드를 보면 된다.
1. 재귀함수
먼저 피보나치 수열은 재귀함수로 쉽게 구현할 수 있는데, 재귀함수는 숫자가 커질수록 시간이 기하급수적으로 늘어난다는 단점이 있다. 시간복잡도가 O(n^2)이다.
[재귀함수를 이용한 코드]
#include <iostream>
using namespace std;
int num0 = 0, num1 = 0;
int fibonacci(int n) {
if (n == 0) {
num0++;
return 0;
} else if (n == 1) {
num1++;
return 1;
} else {
return fibonacci(n-1) + fibonacci(n-2);
}
}
int main()
{
int t;
cin >> t;
for(int i=0; i<t; i++){
num0 = 0, num1 = 0;
int n;
cin >> n;
fibonacci(n);
cout << num0 << " " << num1 << "\n";
}
return 0;
}0과 1을 카운트하기 위한 변수 num0, num1을 전역변수로 선언하고 함수에서 0과 1이 리턴될 때마다 변수를 1씩 증가시킨다. 테스트 케이스가 존재하므로 num0과 num1을 재사용하기 위해 반복문 안에서 0으로 초기화한다. 재귀함수에서 fibonacci(0)과 fibonacci(1)이 호출되는 횟수를 그야말로 직관적으로 확인할 수 있는 기초적인 방법이다. 당연하게도 시간 초과라는 결과가 맞이하러 온다.
2. 메모이제이션(memoization)
메모이제이션은 사람마다 구현하는 방법이 살짝 다르긴하지만, 원리는 간단하다. 비효율적이게 같은 계산을 반복하지말고 계산한 값을 메모리에 저장해서 재사용하자는 뜻이다.
피보나치 수열 : 0 1 1 2 3 5 8 13 21 34 55 ··· (문제에서는 0부터 시작)
fibonacci(6)은 8이고, fibonacci(4)와 fibonacci(5)를 더한 값이다. 즉, 피보나치 수열을 배열에 그대로 저장하면, 배열에서 4번째와 5번째를 꺼내 더하기만 하면 되는 것이다. 그런데 우리는 피보나치 수열을 구하는 게 아니라 0과 1의 호출 횟수를 구해야 한다. 그런데 피보나치 수열의 계산 방식을 잘 생각해보면 호출 횟수에 어떠한 규칙이 있을 거라고 추측할 수 있다. 여기서 1번의 재귀함수 코드를 이용해 0과 1의 호출 횟수가 어떻게 바뀌는지 눈으로 직접 확인해보자.
[0과 1의 호출횟수를 확인하기 위한 코드]
#include <iostream>
#include <cmath>
using namespace std;
int num0 = 0, num1 = 0;
int fibonacci(int n) {
if (n == 0) {
num0++;
return 0;
} else if (n == 1) {
num1++;
return 1;
} else {
return fibonacci(n-1) + fibonacci(n-2);
}
}
int main()
{
int t = 10;
for(int i=0; i<t; i++){
num0 = 0, num1 = 0;
fibonacci(i);
printf("fibonacci(%d): %d %d\n", i, num0, num1);
}
return 0;
}코드를 조금 수정해 fibonacci(0)부터 fibonacci(9)까지 0과 1의 호출 횟수를 출력해봤다.

결과를 확인해보면 fibonacci(0)을 제외하고 피보나치 수열 값과 같다는 것을 알 수 있다. 0의 호출 횟수는 fibonacci(n-1), 1의 호출 횟수는 fibonacci(n)과 같다. 즉, 우리는 피보나치 수열을 빠르게 구하기만 하면 0과 1의 호출 횟수도 함께 구할 수 있다.
[메모이제이션을 이용한 코드]
메모이제이션을 이용할 때 가장 고민했던 부분은 fibonacci(0)일 때의 호출 횟수를 어떻게 처리할까하는 것이었다. 배열을 한칸씩 뒤로 밀고 맨 앞에 1을 삽입하는 방법을 생각해봤는데, 인덱스가 수열과 맞지 않아 헷갈리기 때문에 좋은 코드가 아닌 것 같았다. 그래서 임시방편으로 조건문을 달아 fibonacci(0)의 경우만 따로 출력되도록 했다.
사실 다른 사람들이 구현한 메모이제이션 코드를 보고 따라하면서 의아해지는 부분이 있었는데, 그 부분이 결국 시간에서 발목을 잡았다.
int memo[40] = {0,1,}; // 0번째에 0, 1번째에 1로 초기화
int fibonacci(int n) {
if(n == 0 || n == 1){
return memo[n];
}
if(memo[n]){ // 값이 존재하면 그대로 반환
return memo[n];
}else{ // 0이면 아직 계산이 안 됐으므로 계산한 값을 반환
return memo[n] = fibonacci(n-1) + fibonacci(n-2);
}
}이 코드를 보면 memo[n]에 값이 존재하지 않을 때만 피보나치 함수를 호출한다. 호출 횟수가 획기적으로 줄긴 했으나, fibonacci(n-2)와 fibonacci(n-1)을 호출하기 때문에 이 상태로 제출하면 시간 초과라는 결과가 기다린다. 생각해보면 fibonacci(n-2)는 굳이 한 번 더 호출할 이유가 없다. fibonacci(n-1)을 계산했다면 이미 계산된 값이 memo[n-1]까지 저장되었을 것이다. 그러니 memo[n-2]로 불러내면 된다.
[통과한 코드 - 메모이제이션 사용]
#include <iostream>
using namespace std;
int memo[40] = {0,1,};
int fibonacci(int n) {
if(n == 0 || n == 1){
return memo[n];
}
return memo[n] = fibonacci(n-1) + memo[n-2];
}
int main()
{
int t;
cin >> t;
for(int i=0; i<t; i++){
int n;
cin >> n;
if(n==0){
cout << "1 0\n";
continue;
}
fibonacci(n);
cout << memo[n-1] << " " << memo[n] << "\n";
}
return 0;
}피보나치 함수를 두 번 불러내는 것만으로 시간초과가 나기 때문에, n까지 피보나치 수열을 계산해 배열 memo에 저장해둔다. memo[n-1]과 memo[n] 사이에 공백을 두고 출력하면 통과할 수 있다.

함수를 재귀적으로 불러내지 않고 해결할 수 있는 방법이 하나 더 있다. 재귀라는 방법을 아예 던져놓고 생각해보면, 피보나치 수열은 n-2번째와 n-1번째를 더한 값을 n번째에 저장하는 것이다. 그러면 함수를 불러내지 않고 배열만 사용해 계산할 수 있지 않겠는가? 반복문을 사용해 해결하는 방법이 있다.
#include <iostream>
using namespace std;
int memo[40] = {0,1,};
int fibonacci(int n) {
if(n == 0 || n == 1){
return memo[n];
}
for(int i=2; i<=n; i++){
memo[i] = memo[i-2] + memo[i-1];
}
return memo[n];
}
int main()
{
int t;
cin >> t;
for(int i=0; i<t; i++){
int n;
cin >> n;
if(n==0){
cout << "1 0\n";
continue;
}
fibonacci(n);
cout << memo[n-1] << " " << memo[n] << "\n";
}
return 0;
}2부터 n까지 memo[i-2]와 memo[i-1]를 더하고 memo[n]을 반환한다. 이렇게 되면 피보나치 함수를 한 번만 호출하고, 반복문을 한 번 돈것만큼의 시간복잡도만 발생한다.
참고로 피보나치 함수를 몇 번이나 호출하는지 확인하기 위해 다음과 같은 코드를 추가할 수 있다.
int fibonacci(int n) {
printf("fibonacci(%d) is called.\n", n);
if(n == 0 || n == 1){
return memo[n];
}
return memo[n] = fibonacci(n-1) + memo[n-2];
}
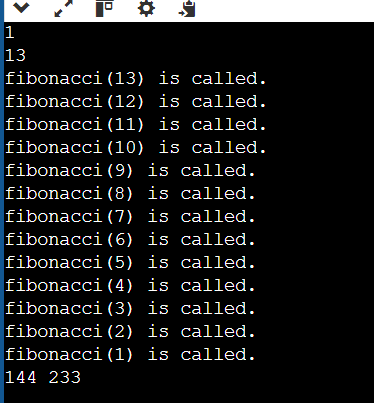
위 코드는 n만큼 함수를 호출한다.
실험을 거듭하며 풀리지 않는 의문점이 있다. 아래 주석처리된 부분을 넣으면 틀리고, 빼면 통과되는데 코드를 돌려봤을 때 결과가 똑같아서 왜 틀리는지 모르겠다. 시간 초과도 아니고 '틀렸습니다'라고 나온다. 해당 코드는 대부분의 메모이제이션에서 사용되는 코드인데, 함수 호출 횟수가 줄어들 뿐 결과가 틀릴만한 부분은 없어 보이는데 원인을 모르겠다.
int fibonacci(int n) {
if(n == 0 || n == 1){
return memo[n];
}
//if(memo[n]) return memo[n];
return memo[n] = fibonacci(n-1) + memo[n-2];
}값이 이미 존재하면 그대로 반환하는 코드

참고
